Verification of a reader-writer lock with TLA+

A concurrent program is like a complicated state machine: the number of possible states increases exponentially with the number of threads and steps in the program logic. Reasoning about it can get quickly out of hand. It’s hard to make sure that subtle bugs are not lurking in the code. What’s more, issues related to concurrency are the kind that reveal themselves at the worst possible moment, typically when scaling the system in production.
Formal verification
Formal verification is a powerful tool that can help in gaining confidence about a concurrent or distributed system. It can also reveal very tricky bugs that would only appear under higher load, precisely at the worst possible moment. There are a number of formal verification methods out there: Coq (INRIA), Alloy, TLSA, and of course the one we are covering here. TLA+ was invented in 1999 by Leslie Lamport, who is also the inventor of the Paxos algorithm and LaTeX among other major contributions. The language has been notoriously adopted by Amazon Cloud for verification of some aspects of the distribution algorithms behind DynamoDB’s strong consistency guarantees. TLA+ has a simplified C-like syntax named PlusCal, for which a good tutorial can be found here.
TLA+
Using PlusCal, one basically describes a concurrent program with a model defining a number of processes, each going through a sequence of steps identified by labels. Labels represent units of atomic execution. The model checker walks through the domain of all possible executions of processes and looks for traces leading to deadlocks, broken invariants or violated assertions. It can also verify that the program progresses and terminates.
Reader-writer lock
A topic we cover in my concurrent programming teaching assignment are reader-writer locks. We have an exercise in particular where we generalize this concept slightly and consider threads of two classes, A and B (rather than reader/writer). Threads of one class can access the resource concurrently, whereas threads of different classes cannot. Since this is a relatively simple piece of code involving some semaphores, I decided to use this exercise to take TLA+ for a spin. Here’s the C++ implementation that we will try to prove. It uses Qt’s QSemaphore, with acquire() and release() methods only:
#include <QSemaphore>
#include <iostream>
class ReaderWriterClassAB
{
protected:
QSemaphore mutexA;
QSemaphore mutexB;
QSemaphore resourceMutex;
int aCount;
int bCount;
void lock(QSemaphore& mutex, int& count)
{
mutex.acquire();
count++;
if (count == 1)
{
resourceMutex.acquire();
}
mutex.release();
}
void unlock(QSemaphore& mutex, int& count)
{
mutex.acquire();
if (count <= 0) // if it wasn't locked
{
mutex.release();
return;
}
count--;
if (count == 0)
{
resourceMutex.release();
}
mutex.release();
}
public:
ReaderWriterClassAB(): mutexA(1), mutexB(1), resourceMutex(1), aCount(0),
bCount(0)
{
}
void lockA()
{
lock(mutexA, aCount);
}
void unlockA()
{
unlock(mutexA, aCount);
}
void lockB()
{
lock(mutexB, bCount);
}
void unlockB()
{
unlock(mutexB, bCount);
}
};
Corresponding specification
Here’s the full corresponding TLA+ specification below (or at least how I managed to translate it). We’ll look at it step by step next.
------------------- MODULE classab -----------------------
EXTENDS Integers, TLC, Sequences
(* --algorithm classab
variables
aSem = 0,
bSem = 0,
a = 0,
b = 0,
resourceSem = 0,
aInside = 0,
bInside = 0,
aIter = 0,
bIter = 0;
macro lock(sem) begin
await sem = 0;
sem := sem + 1;
end macro
macro unlock(sem) begin
sem := sem - 1;
end macro
fair process classA \in 1..2
begin
Iterations:
while aIter < 5 do
aIter := aIter + 1;
LockEntry:
lock(aSem);
IncreaseCount:
either
a := a + 1;
or
a := a - 10; rectifyInc: a := a + 11;
end either;
MaybeLockResource:
if (a = 1) then
lock(resourceSem);
end if;
UnlockEntry:
unlock(aSem);
ClassExclusiveAccess:
aInside := aInside + 1;
assert bInside = 0;
LockEntry2:
lock(aSem);
DecreaseCount:
either
a := a - 1;
or
a := a + 10; rectifyDec: a := a - 11;
end either;
MaybeUnlockResource:
aInside := aInside - 1;
if (a = 0) then
unlock(resourceSem);
end if;
UnlockEntry2:
unlock(aSem);
end while;
end process
fair process classB \in 3..4
begin
Iterations:
while bIter < 5 do
bIter := bIter + 1;
LockEntry:
lock(bSem);
IncreaseCount:
either
b := b + 1;
or
b := b - 10; rectifyInc: b := b + 11;
end either;
MaybeLockResource:
if (b = 1) then
lock(resourceSem);
end if;
UnlockEntry:
unlock(bSem);
ClassExclusiveAccess:
bInside := bInside + 1;
assert aInside = 0;
LockEntry2:
lock(bSem);
DecreaseCount:
either
b := b - 1;
or
b := b + 10; rectifyDec: b := b - 11;
end either;
MaybeUnlockResource:
bInside := bInside - 1;
if (b = 0) then
unlock(resourceSem);
end if;
UnlockEntry2:
unlock(bSem);
end while;
end process
end algorithm; *)
Locking
Let’s look at the various parts of the specification, without entering into details of the syntax (for more information, I highly recommend the aforementioned tutorial). After variable declaration, we find a first interesting definition:
macro lock(sem) begin
await sem = 0;
sem := sem + 1;
end macro
Macros are bits of specification that get inlined and allow sharing specification logic. This macro simulates locking of a semaphore: the first line in particular: await sem = 0; makes use of the await keyword to indicate blocking on a condition.
The following macro does the reverse operation:
macro unlock(sem) begin
sem := sem - 1;
end macro
Multi-threading
The second part describes the processes involved, that is the threads in our case. The declaration fair process classA \in 1..2 defines our thread of class A, with two instances (“1” and “2”). Combined with the other process declaration below fair process classB \in 3..4, this defines four threads, two of each class. As you can see, it is easy to change this to simulate more threads - but that will be at the cost of checker time, since more threads means exponentially more states to be checked.
Memory access
Thanks to the labels, process specification is rather self-explanatory when putting it side-to-side with the C++ program. One bit worthy of mention is the following:
IncreaseCount:
either
a := a + 1;
or
a := a - 10; rectifyInc: a := a + 11;
end either;
What this does is simulate memory access contention on the a variable! The either or notation defines that execution can follow both paths. As can be seen in this case, the second path a := a - 10; rectifyInc: a := a + 11; describes two separate execution steps. After the first intermediary step, the variable value is effectively in a (transient) invalid state. If some other execution path is able to access the value at this point (which the checker will verify when exploring the state set), the whole specification would fail. Therefore, this validates our critical section (we’ll simulate this problem below).
Specification checking
It is now time to move on to verifying our model. The screenshot below shows some of the options in the TLA+ IDE:
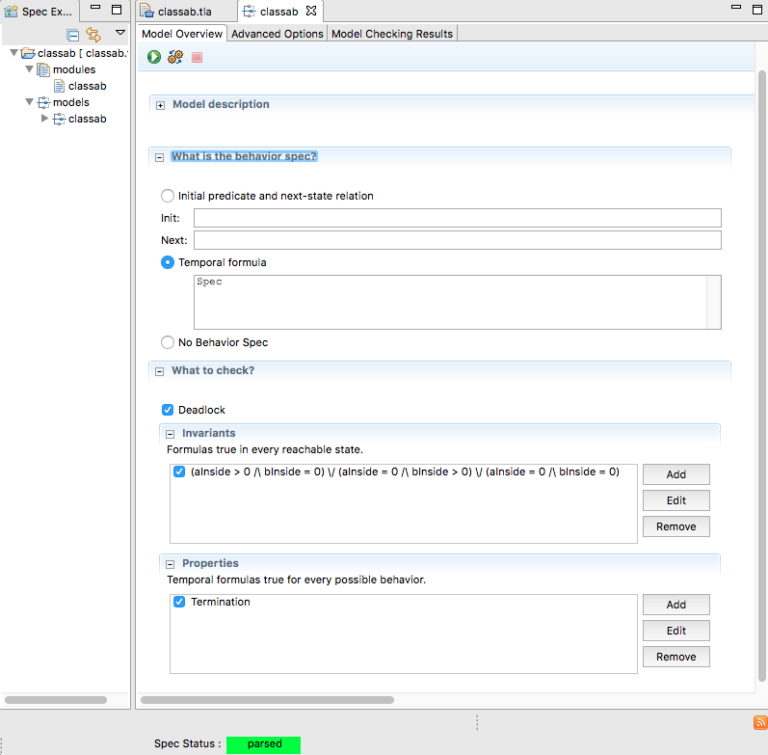
As can be seen in the screenshot, we can verify the following properties:
- absence of deadlock
- custom invariant: at any point in time in the execution, the
(aInside > 0 /\ bInside = 0) \/ (aInside = 0 /\ bInside > 0) \/ (aInside = 0 /\ bInside = 0)must be true. In wording, this means that only three states are possible throughout the execution: either A threads have exclusive access to the resource, or B threads have exclusive access, or no one has access. - termination: this checks that the program actually completes and doesn’t run in circles at some point in the execution with for instance a livelock.
Running the checker leads to the following output:
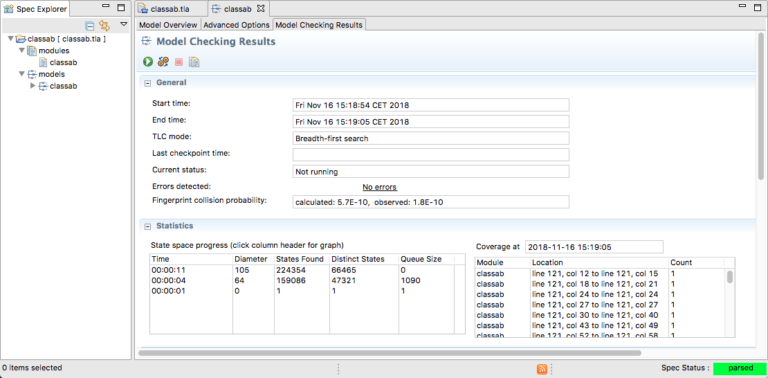
Hurray! no errors were found. The other interesting metrics that are visible in the results screen are the following:
- Diameter: 105 - the number of steps of the longest execution
- States found: 224’354 - total number of states that were explored
- Distinct states: 66’465 - out these states, which had different variable values
For such a small program, it is amazing to see that we can already end up traversing more that sixty-thousand distinct states! No wonder that concurrent programming is difficult.
Errors
Let’s be a bit naughty and find out how the checker behaves in the presence of errors.
Breach of mutual exclusion
If we comment out resource locking in process A:
\* MaybeLockResource:
\* if (a = 1) then
\* lock(resourceSem);
\* end if;
The checker ends up failing one of our assertions after 11 steps:
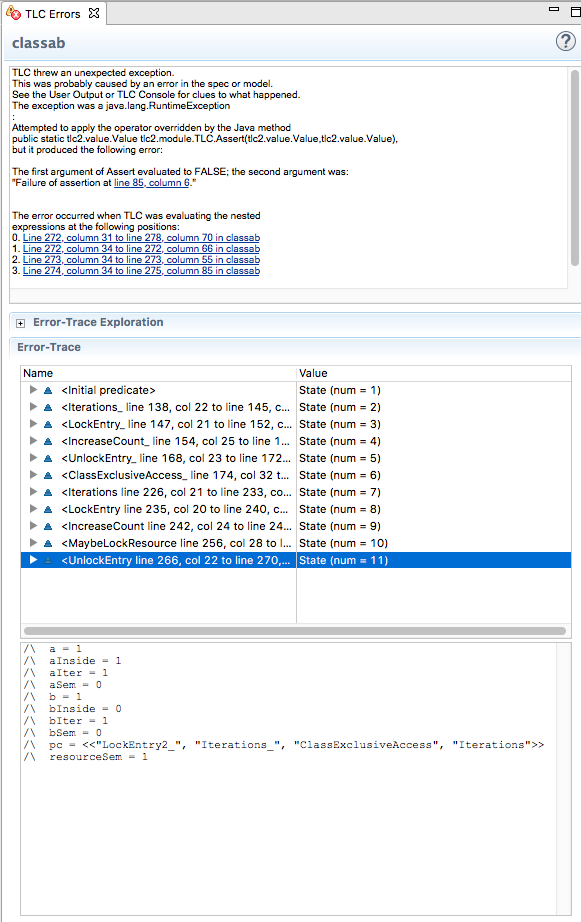
The failing assertion, not surprisingly, is in the B process, where we check whether B is also inside with the line assert aInside = 0;. Following the trace allows finding out the sequence of steps that lead to the issue: transposing this to real code, this would be our exact recipe to reproduce the bug!
If we remove the assertion, the global invariant that we defined in the checker properties also fails, as we expect:
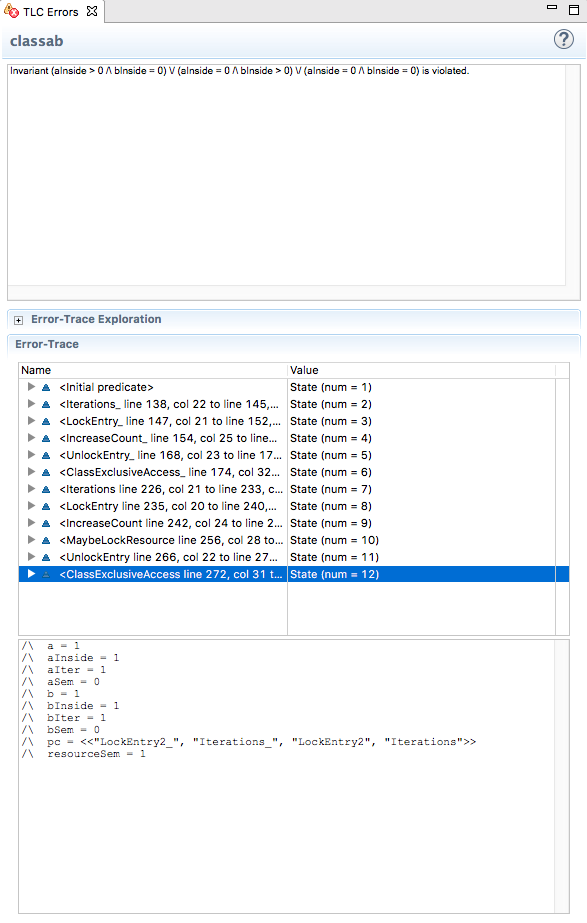
Interestingly, if we now remove all invariants or assertions that verify mutual exclusion, we end up in a deadlock after 52 steps. This was to be expected since we did not comment out the corresponding semaphore unlocking in threads of class A. When the A threads have performed unnecessary “unlocks” a sufficient number of times, the value of the resourceSem semaphore is decreased below zero to the point that B threads can no longer get in and the program gets stuck:
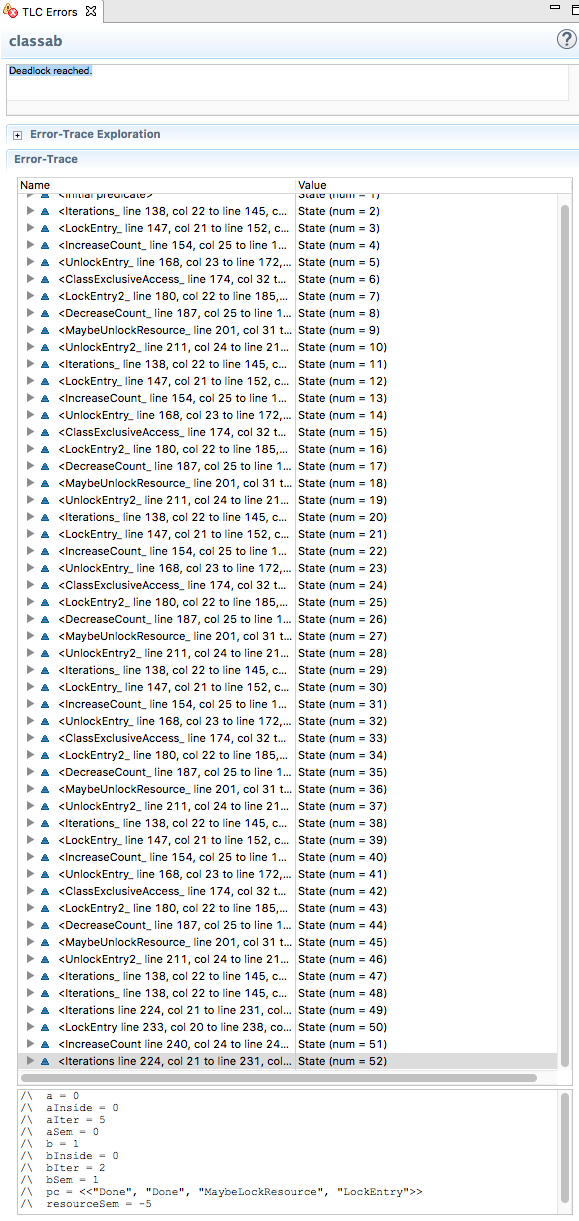
Conclusion
In this short example, we have seen the potential of TLA+ to simulate and verify execution of a concurrent program. Putting together a specification does represent some time investment. But going through the effort of modelling the execution helps in reflecting about possible concurrent issues and in gaining more understanding of code behaviour. It allows exploring alternatives, documents the design and obviously is able to find very tricky bugs, which is why it is in use at Amazon. Although awkward at times, the syntax felt somewhat familiar for a coder like me. The specification has a feel of property-based unit testing, with much more expressiveness: it’s all about defining the logic domain and the execution search space.